基于改进的CORDIC算法的FFT复乘及其FPGA实现

文章摘要：这样分解后，被旋转向量与K的乘转化为简单的移位加减运算，从而可以解决乘法器一级速度变慢而降低整个流水线吞吐率的问题。其硬件实现结构如图2所示。这种结构进一步降低了硬件复杂度，与前面的流水线CORDIC结构相似，使整体结构更加规则统一，有利于VLSI实现。4 FFT复乘的FPGA实现 由于软件和DSP实现的速度较慢，而FPGA资源丰富，组织结构便于采用流水线结构和并行运算，其速度快、扩展能力强，所以CORDIC算法的移位、加减法运算和流水线结构更容易在FPGA上实现。本文在ALTEra公司的QuartusⅡ7.2软件环境下使用VHDL，利用上述各种算法设计了16 bit宽的FFT复乘模块并

基于改进的CORDIC算法的FFT复乘及其FPGA实现,标签：电路设计,http://www.88dzw.com

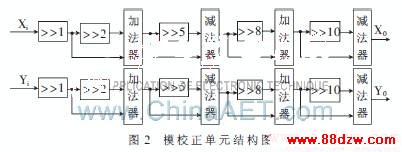
这样分解后，被旋转向量与K的乘转化为简单的移位加减运算，从而可以解决乘法器一级速度变慢而降低整个流水线吞吐率的问题。其硬件实现结构如图2所示。这种结构进一步降低了硬件复杂度，与前面的流水线CORDIC结构相似，使整体结构更加规则统一，有利于VLSI实现。

4 FFT复乘的FPGA实现
    由于软件和DSP实现的速度较慢，而FPGA资源丰富，组织结构便于采用流水线结构和并行运算，其速度快、扩展能力强，所以CORDIC算法的移位、加减法运算和流水线结构更容易在FPGA上实现。本文在ALTEra公司的QuartusⅡ7.2软件环境下使用VHDL，利用上述各种算法设计了16 bit宽的FFT复乘模块并在CycloneⅡ EP2C35F672C6芯片上进行验证。
    图3为改进的16级流水线结构的CORDIC算法实现复乘模块的顶层结构图，address为ROM的地址，Xi_re、Xi_im为输入序列的实部和虚部，Xo_re、Xo_im为旋转后的实部和虚部。输入数据为16 bit宽，为提高精度，对所有内部信号及输出信号都用20 bit的补码。整个复乘主要由系数ROM、预旋转、16级流水线CORDIC迭代、系数寄存器和模校正因子K 5个模块组成。

    小，但不能完全消除。

    图5为改进的CORDIC算法实现FFT复乘资源消耗与最高工作速度情况。传统的复乘要4个乘法器，所以传统的复乘要实现16 bit位宽复乘需用此芯片中的8个9 bit乘法单元，而从资源消耗情况来看，改进的CORDIC算法实现此复乘没有用乘法器，整个逻辑单元消耗也只有4%；另外基于改进的CORDIC算法的复乘最高工作频率达到了190 MHz，与传统CORDIC算法的复乘速度（约130 MHz）相比有较大提高，在节约资源的同时提高了工作速度。

    本文利用定点FFT复乘运算中旋转因子的旋转系数可预先求出的特点，采用改进流水线结构的CORDIC算法，与传统的CORDIC算法的复乘相比，不仅不需要乘法器实现了FFT运算中序列与旋转因子的复数乘运算，并且在节约资源的同时提升了工作速度。这种基于改进的CORDIC算法的复乘运算对提高FFT处理器的速度和减少资源消耗有较大意义。同时，利用VHDL语言，采用模块化设计思想，使得本设计可移植性强、通用性好，只需作少量改动（如增加位宽，增加迭代次数），便可满足精度上的更高要求，具有一定的工程实际意义和应用前景。

上一页  [1] [2] [3]  下一页