卡诺图的构成及其简法

文章摘要：图2．6 函数F(A,B,C)=∑m(1,2,3,7)的卡诺图 2．逻辑函数为一般“与-或”表达式 当逻辑函数为一般“与-或”表达式时，可根据“与”的公共性和“或”的叠加性作出相应卡诺图。 例如，4变量函数F(A,B,C,D)=AB+CD+A·BC的卡诺图如图2．7所示。图2．7 函数F(A,B,C,D)=AB+CD+A·BC的卡诺图 填写该函数卡诺图时，只需在4变量卡诺图上依次找出和“与项”AB、CD、A·BC对应的小方格填上1，便可得到该函数的卡诺图。 当逻辑函数表达式为其他形式时，可将其变换成上述形式后再作卡诺图。 为了叙述的方便，通常将卡诺

卡诺图的构成及其简法,标签：电子电路基础,模拟电路基础,http://www.88dzw.com

图2．6 函数F(A,B,C)=∑m(1,2,3,7)的卡诺图

    
    2．逻辑函数为一般“与-或”表达式

    当逻辑函数为一般“与-或”表达式时，可根据“与”的公共性和“或”的叠加性作出相应卡诺图。
    例如，4变量函数F(A,B,C,D)=AB+CD+A·BC的卡诺图如图2．7所示。

图2．7  函数F(A,B,C,D)=AB+CD+A·BC的卡诺图


    填写该函数卡诺图时，只需在4变量卡诺图上依次找出和“与项”AB、CD、A·BC对应的小方格填上1，便可得到该函数的卡诺图。
    当逻辑函数表达式为其他形式时，可将其变换成上述形式后再作卡诺图。

    为了叙述的方便，通常将卡诺图上填1的小方格称为1方格，填0的小方格称为0方格。0方格有时用空格表示。

    四 卡诺图上最小项的合并规律
    卡诺图的一个重要特征是，它从图形上直观、清晰地反映了最小项的相邻关系。当一个函数用卡诺图表示后，究竟哪些最小项可以合并呢？下面以2、3、4变量卡诺图为例予以说明。

    1．两个小方格相邻, 或处于某行(列)两端时，所代表的最小项可以合并，合并后可消去一个变量。

    例如，图2.8给出了2、3、4变量卡诺图上两个相邻最小项合并的典型情况的。



图2．8 两个相邻最小项合并的情况

    2．四个小方格组成一个大方格、或组成一行（列）、或处于相邻两行（列）的两端、或处于四角时，所的表的最小项可以合并，合并后可消去两个变量。

    例如，图2.9给出了3、4变量卡诺图上四个相邻最小项合并的典型情况的。


图2．9 四个相邻最小项合并的情况
    3．八个小方格组成一个大方格、或组成相邻的两行（列）、或处于两个边行（列）时，所代表的最小项可以合并，合并后可消去三个变量。

    例如，图2．10给出了3、4变量卡诺图上八个相邻最小项合并的典型情况的。



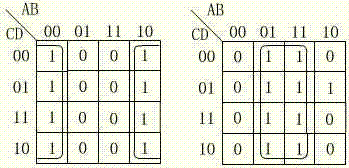
图2．10 八个相邻最小项合并的情况
    至此，以3、4变量卡诺图为例，讨论了2，4，8个最小项的合并方法。依此类推，不难得出n个变量卡诺图中最小项的合并规律。

    归纳起来，n个变量卡诺图中最小项的合并规律如下：

    （1）卡诺圈中小方格的个数必须为2m个，m为小于或等于n的整数。
    （2）卡诺圈中的2m个小方格有一定的排列规律，具体地说，它们含有m个不同变量，(n-m)个相同变量。
    （3）卡诺圈中的2m个小方格对应的最小项可用(n-m)个变量的“与”项表示，该“与”项由这些最小项中的相同变量构成。
    （4）当m=n时，卡诺圈包围了整个卡诺图，可用1表示，即n个变量的全部最小项之和为1。

上一页  [1] [2] [3]  下一页